前回の記事では引用行動の理由についてまとめてみました。
今回の記事では引用回数という指標をどう扱うのか、引用回数を用いたジャーナル指標について定義と問題点、その使用方法についてみていきたいと思います。
中々普段わざわざ調べる余裕がないんじゃないかと思いますので、ぜひ参考にしてもらえますと嬉しいです。
特に代表的なインパクトファクター(IF;正式名称はジャーナルインパクトファクター)は論文やジャーナルの評価指標として広く知られていますが、実際それだけではカバーしきれない多様な視点があります。IFについては以前の記事でまとめています。
そこで本記事では、IF以外の指標について詳しく掘り下げて紹介します。また、Google検索のアルゴリズム「PageRank」を応用した指標や、個別の研究者や論文を評価する指標についても解説します。
今回の内容は以下のYouTube動画の後半から作成しています。ぜひこちらもどうぞ。
- IF以外の代表的なジャーナル指標
- CiteScore:JIFに類似しているが透明性が高くオープンな指標
- Journal Citation Indicator (JCI):分野間比較を目指す指標
- SNIP:分野ごとの引用慣習を考慮
- PageRankの仕組みと応用:EigenfactorとSJR
- Eigenfactor:PageRankアルゴリズムを応用した指標
- Scimago Journal Rank (SJR):ScopusベースでPage rankを使った指標
- h-indexとAltmetrics:研究者や論文の評価指標
- h-index:研究者やジャーナルの長期的な影響力を評価
- Altmetrics:一般社会的な影響を測定
- まとめ:ジャーナル指標を適切に活用するために
- 参考文献
IF以外の代表的なジャーナル指標
まずは、IFの代替や補完として用いられる代表的なジャーナル指標を紹介します。これらは、IFの課題に対応する形で開発されており、それぞれ独自の特徴を持っています。
- CiteScore
- Journal Citation Indicator (JCI)
- Source Normalized Impact per Paper (SNIP)
- Eigenfactor
- Scimago Journal Rank (SJR)
これらの指標は、ジャーナル全体の影響力を測るために設計されていますが、対象となるデータベースや計算方法、評価基準が異なります。以下では、それぞれの指標について詳しく解説します。
CiteScore:JIFに類似しているが透明性が高くオープンな指標

CiteScoreは、エルゼビア社のデータベース「Scopus」を基に算出される指標で、2016年から運用されています。インパクトファクター(IF)と非常に似た計算方法を採用していますが、いくつかの違いがあります。
CiteScoreの特徴
- データベースの範囲が広い
Scopusに登録されているジャーナル数はWeb of Science(IFのデータベース)よりも多いため、計算結果が異なる場合があります。 - 無料でアクセス可能
IFはClarivate社との契約が必要ですが、CiteScoreは誰でも無料でデータを閲覧可能です。計算に使われた引用数や対象論文もオープンに公開されています。 - 計算期間の違い
CiteScoreは過去4年間の引用回数を基に計算され、IFの2年間よりも長期間を対象としています。 - 分母と分子の一致
IFでは引用対象(分子)と総出版数(分母)に差がありましたが、CiteScoreでは分母と分子が一致しており、計算がより公平です。この問題は総合誌(ニュース記事などを含む)が有利になりやすいといった点につながっています。詳しくはIFについて述べた過去記事を参照してください。
例えば、2023年の主要ジャーナルのスコアを比較すると以下のようになります。
| ジャーナル名 | CiteScore | IF |
|---|---|---|
| Nature | 90 | 50.5 |
| Cell | 110 | 45.6 |
| Lancet | 148.1 | 98.4 |
| NEJM | 145.4 | 96.3 |
この結果から、NatureとCellのスコアが逆転していることがわかります。これは計算対象期間やデータベースの違いによるものですが、CiteScoreの分母と分子が一致している点も影響していると考えられます。
問題点
ただし、CiteScoreも完全ではありません。基本的にはIFと類似しているため、同じ問題がそのまま残っています。総合誌が有利になりやすい問題はないとしても、研究分野ごとで有利不利が異なるといった点や、reviewが多い雑誌の方が引用されやすいため有利になる、といった点は残ります。また、算出元がエルゼビア社という出版社であるため、Cellなどに有利になるような方法論を組みやすいのではないか、と勘繰ってしまう部分はありますね。ただ、計算方法も含めてオープンにはなっていますので透明性は十分担保されていると思います。
Journal Citation Indicator (JCI):分野間比較を目指す指標

Journal Citation Indicator (JCI)は、Clarivate社が2021年から提供を開始した新しい指標です。特徴は、分野や発行年による引用回数のばらつきを補正し、分野を超えた比較を可能にする点です。
JCIの特徴
- 標準化されたスコア
各ジャーナルの引用回数を分野ごとの世界平均(1.0)で標準化して算出。スコア2.0であれば、平均の2倍引用されていることを意味します。 - 引用対象の限定
ArticlesやReviewsを対象とし、分母と分子を一致させています。IFの問題点は解決されているわけですね。また、計算対象期間は3年間です。 - レビュー記事の優遇を軽減
IFではレビュー記事が多いジャーナルが有利になりがちでしたが、JCIではレビューと研究論文を区別して計算しています。
問題点
JCIも引用回数に基づく指標ではあるため、一部のトップ論文がジャーナル指標全体の数値を引っ張ってしまう問題が残ります。つまりジャーナルとしての指標の数値が高くても論文の評価には直接的に影響しません。これはどの指標でも持つ問題点だとは思います。
また、対象がArticlesとReviewsに限定されているため、逆に言えばそれ以外の論文の影響力は評価されません。
SNIP:分野ごとの引用慣習を考慮

Source Normalized Impact per Paper (SNIP)は、オランダのライデン大学のチームが開発した指標で、分野ごとの引用慣習を考慮して補正する仕組みが特徴です1。ウェブページで雑誌ごとの数値も細かく確認できるようになっています。
SNIPの特徴
- 引用慣習の補正
分野ごとのdatabase citation potential(DCP)と言われる引用回数の可能性を評価した数値を用いて補正しています。例えば、生命医学のように引用数が多い分野ではDCPが大きくなる分スコアが小さくなり、比較が公平になります。 - 調和平均を採用
DCPの計算には算術平均ではなく調和平均を使用し、外れ値の影響を抑えています2。 - オープンアクセス
指標の計算方法やデータは公開されており、誰でも数値を確認できます。学術研究であるため、論文で細かく手法も公開されており、透明性も高いといえます。
問題点
SNIPも引用回数に基づくため、一部の論文がジャーナル指標を押し上げてしまう問題は解決されていません。しかし、分野間での公平性を高まっている点では有用な指標と言えます。
PageRankの仕組みと応用:EigenfactorとSJR
PageRankは、Googleの検索エンジンで使用されているアルゴリズムで、ウェブページの重要性をリンク構造から評価する仕組みです。このアルゴリズムが引用ネットワーク分析にも応用され、EigenfactorやScimago Journal Rank (SJR)といった指標の基礎となっています。
また以前に紹介したIncitefulという論文のネットワーク可視化ツールでもこのページランクは使われています。
なので、まずPageRankアルゴリズムから簡単に紹介します。
PageRankの基本的な仕組み
PageRankのアルゴリズムは以下のステップで行っていきます。下の図を参考にしながら考えてみましょう:
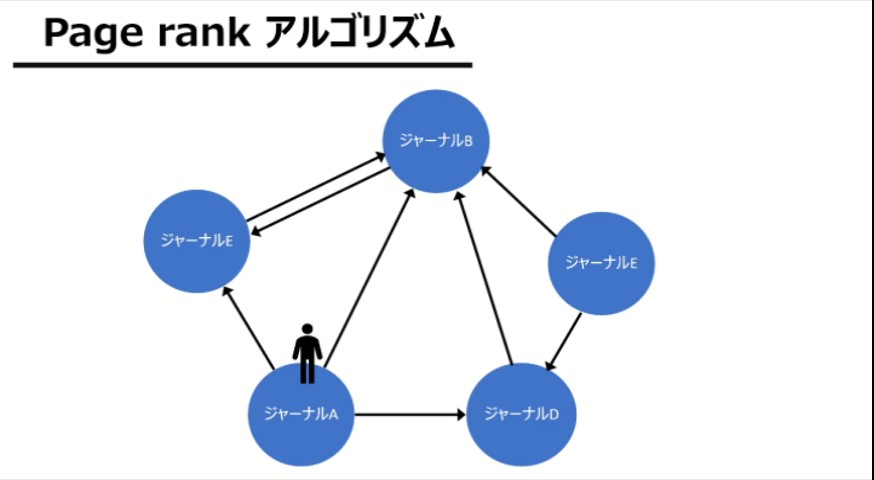
- 引用をネットワークとして捉える
各ジャーナルを「ノード(点)」として配置し、引用関係を「エッジ(矢印)」で表現します。たとえば、図のようにジャーナルAがジャーナルBを引用していれば、AからBに向かう矢印が引かれます。 - ランダムウォーク(確率的移動)
ネットワーク内でランダムにジャーナルを「移動」する読者を想定します。初期の点はそれぞれ等確率で設定します。上図の5つのジャーナルだったらそれぞれのジャーナルに読者がいる確率は1/5です。
ここで、たとえば、読者がジャーナルAの論文を読み、その論文が引用している別のジャーナルを読むと仮定します。例えばジャーナルBからの引用が多ければ、ジャーナルBを読む確率は上がるようになっています。このように引用をたどって読者が使う時間をシミュレーションしているわけです。あとは確率的な移動をひたすら繰り返します。 - 重み付け
上記の仕組みのため、より多くのジャーナルから引用されているジャーナル(図で言うとジャーナルB)は重要度が高いとされます。また、重要なジャーナルから引用されているジャーナルは、そこへの移動確率も当然上がりますので高いランクを得ることができます。。 - 収束
このランダムウォークを繰り返すことで、最終的に各ジャーナルに「滞在する確率」が収束します。この確率がPageRankスコアとなります。
より詳しく計算背景について知りたい方は英語ですがこちらのYouTube動画がオススメです3。要するに各ノードと遷移確率を設定した行列計算を繰り返していくことで最終的な値が確認できるようになっています。いわゆるマルコフ過程となっている(つまり遷移確率について前にどのジャーナルを読んでいたかは関係ない)ので、MCMC法など勉強し慣れている人は雰囲気はすぐわかるのではないかと思います。
ちなみに他のジャーナルを引用しないジャーナルや本が存在する場合、そこに閉じ込められてしまい、このランダムウォークが止まってしまいます。これはdangling node(「ぶら下がりノード」)と呼ばれており、この問題を解決するため、常に一定の低確率で他のジャーナルにジャンプする仕組みが導入されています。
これから紹介するジャーナル指標の計算式をみると必ずこのジャンプの確率が組み込まれていますが、これはdangling node対策となっています。
Eigenfactor:PageRankアルゴリズムを応用した指標

Eigenfactorは、PageRankアルゴリズムを応用したジャーナル指標です。Clarivate社の「Web of Science」をデータベースとして利用し、過去5年間の引用データを基に算出されます。特徴的なのは、単なる引用回数ではなく、引用元ジャーナルの重要性を考慮して重み付けを行う点です。
特徴
- 引用の質を評価
単なる引用回数ではなく、他のジャーナルからどのように引用されているかを重視します。たとえば、影響力の高いジャーナル(例:Nature)から引用された場合、より高い重みが付与されます。 - 自ジャーナル引用の影響を除外
ページランクアルゴリズムでは引用元も考慮するため自ジャーナルの引用はカウントされません。そのため編集者が意図的に指標の数値を上げようとする操作が難しくなっています。
IFとの違いの例
面白い例として実際の数値からIFとの違いをみてみましょう。がん研究に特化したジャーナル「CA: A Cancer Journal for Clinicians」は、がんの統計や第3相試験と呼ばれる薬剤の承認に必要な大規模臨床試験の論文が載っています。そのため、雑誌に載っている論文数が少ないのに対し、引用回数が非常に多いため、2023年のインパクトファクター(IF)は521.6と極端に高くなっています。Natureの2023年のIFは50.5でしたので、これがいかに高いか分かります。10倍です、10倍4。
実際、総論文数をみてみるとCAが80に対してNatureは3263ですので、全然違います。こうなるとIFが上がりやすいのも納得できます。
一方で、Eigenfactorは引用の重みづけが異なるため、総引用回数が多くても全く数値が変わります。なんとCA 0.00823に対してNature 1.02413と大きく逆転しています!100倍以上ですね。
こうして視点を変えて評価してみることも大事なことが分かります。
問題点
- 総引用数に引っ張られる
Eigenfactorは論文一つ当たりの引用回数には依存しない特徴を持ちながらも、結局ジャーナルの総引用回数との相関が強いことが指摘されています5。先ほどのNatureの例のように論文数が多くて引用回数が総合的に多いと結局数値が上がってしまうわけですね。 - データ欠損の影響
引用ネットワーク全体を基に算出するため、データの欠損やジャーナル名の変更が関連するジャーナル群全体に大きな影響を与える可能性があります。
1の問題を緩和するために、Eigenfactorをジャーナルの掲載論文数で割った「Article Influence Score」が開発されましたが、これにより先ほどのCAのような論文数が少ないジャーナルが再び有利になるという課題があり、結局すべてを解決することはできないようです。
Scimago Journal Rank (SJR):ScopusベースでPage rankを使った指標

Scimago Journal Rank (SJR)は、Scopusデータベースを基にした引用指標で、Eigenfactorと同様にPageRankアルゴリズムを採用しています。3年間のデータを用いて計算され、引用元の質を重視する仕組みを持っています。
特徴
- 論文数で補正
SJRは掲載論文数で割る調整が行われており、過剰な引用回数に引っ張られることを抑えています。 - 分野間の比較を可能にする調整
分野の近いジャーナル間の引用の重みを高める仕組みを取り入れています。
問題点
- IFとの相関が強い
掲載論文数で補正を行うため、先ほどのArticle Influence Scoreと同様の問題を抱えます。つまりPageRankアルゴリズムというわざわざ複雑なシステムを採用しているにもかかわらず、IFと似通ってしまうわけです。実際、IFと相関が強いことも指摘されています6。 - データの欠損による影響
Eigenfactorと同様に、データの欠損がネットワーク全体に影響を及ぼします。
h-indexとAltmetrics:研究者や論文の評価指標
さてここからはおまけで個別の研究者や論文を評価する指標も紹介します。代表例としてh-indexとAltmetricsをみてみましょう。
h-index:研究者やジャーナルの長期的な影響力を評価
h-indexは、研究者やジャーナルの成果を、論文数と引用数の両面から評価する指標です。具体的には、「少なくともh回引用された論文がh本以上存在する場合、その研究者やジャーナルのh-indexはhである」と定義されます7。表現として分かりにくいですね笑
例えばAさんの業績が
- 論文1 2回引用
- 論文2 3回引用
- 論文3 100回引用
だったとすると「少なくとも2回引用された論文が2本以上存在する」と言えますので、この人のh-indexは2とされます。ここではh=3は当てはまらないことが分かりますね。論文数とそれぞれの引用回数が分かれば簡単に算出できるのが強みです。
特徴
- 論文数と引用数を両方考慮することで極端な例を排除
引用回数が多い単一の論文(いわゆる「一発屋」)や、全く引用されない多数の論文があっても、h-indexに過剰な影響を与えることはありません。 - 長期的な研究の影響力を測定する指標として優れている。
- 研究者個人だけでなく、ジャーナル全体の評価にも応用可能。
問題点
- 若手研究者に不利
キャリアの浅い研究者は論文数が少ないため、h-indexは低くなりがちです。 - 分野ごとの差異
引用慣習や論文の出版頻度が分野ごとに異なるため、分野間比較には適していません。 - 自己引用の影響
h-indexを計算する際に自己引用を除外するかどうかで、数値が大きく変わる場合があります。
h-indexはあくまで「目安」として利用すべきであり、研究者間で直接比較することには慎重さが求められます。
Altmetrics:一般社会的な影響を測定
Altmetrics(オルトメトリクス)は、従来の引用数に代わり、論文がウェブ上でどのように取り上げられているかを測定する指標です。主に、SNSやブログ、ニュースメディア、特定の研究共有プラットフォームでの言及数を基に算出されます。
特徴
- ウェブ上での反響を数値化
Altmetricsは、TwitterやFacebookなどのSNS、RedditやMendeleyのような学術的プラットフォームでの反響を反映します。論文のページに表示されるカラフルなバッジが特徴的で、クリックすると具体的な引用元を確認できます。 - 学術的引用ではない情報もカバー
一般読者やメディアからの注目度を測ることができ、論文の社会的影響力を評価する指標として役立ちます。
利点
- 研究の即時性を評価できる。SNSやニュースで取り上げられることで、研究がどのように広がっているかをリアルタイムで把握可能。
- 社会的影響力を測定する補助的な指標として有用。
問題点
- 正式な学術評価には限定的
Altmetricsは学術的な引用ではないため、学問的な意義を直接的に測る数値としては信頼しがたいものがあります。 - バイアスの影響
SNSやメディアの注目を集めやすい話題性のある研究が過剰に評価される傾向があります。 - プラットフォームに依存
Altmetricsのスコアは利用されるプラットフォームや地域、文化の違いによって左右されるため、どうしても普遍性に欠けます。
Altmetricsは従来の指標では測りにくい「社会的な注目度」を測定する手段として有用ですが、論文や研究者の価値を評価するものではないといえます。
まとめ:ジャーナル指標を適切に活用するために
前回・今回の記事では、様々なジャーナル指標の特徴と課題について解説してきました。それぞれの指標には、データベースや計算方法の違いにより独自の利点と欠点があります。以下にポイントをまとめます。
指標ごとの特徴と課題
- CiteScore
IFと似た計算方法を採用していますが、引用の対象と分母が一致しているため、総合誌が過剰に有利になるIFの問題を緩和しています。一方で、他の欠点(例:引用回数の偏り)はIFと共通しています。 - Journal Citation Indicator (JCI) と SNIP
分野ごとの引用慣習の違いを補正することで、分野間の比較を可能にしています。ただし、引用の「質」を十分に反映することはできず、引用回数に大きく引っ張られる傾向が残ります。 - Eigenfactor と SJR
PageRankアルゴリズムを応用することで、引用元のジャーナルの影響力を考慮しています。ただし、論文数で調整を行うとIFに近い結果になることが多く、引用回数の影響から完全に脱却することは難しいです。
指標を活用する際の重要なポイント
- 指標の計算方法を理解し、適切に使い分ける
各指標の設計目的や特徴を理解することで、分野や目的に応じた比較が可能になります。ただし、指標を盲信するのではなく、「どのデータを元にしているのか」「何を評価しているのか」を意識することが重要です。 - 引用行動の質を完全に測ることは困難
自己引用やレビュー記事への偏りなどはある程度判別できますが、社会的な要因や学術的必要性以外の理由による引用を完全に分析することは現状では難しいです。そのため、引用数の多さが必ずしも質を保証するものではないことに留意する必要があります。 - AIによる引用内容の解析との組み合わせ
AI技術の発展により、引用内容を解析するツール(例:Sciteなど)が登場しています。こうしたツールを活用することで、引用の背景や意図をより深く理解できる可能性は今後広がっていくのではないでしょうか。
前回記事と合わせてのまとめ
ジャーナル指標を活用する際には、単なる数値を追うのではなく、その背景にある理由を考えるとより楽しんでみられるのではないかと思います。今回見たCAとNatureの例のように一つの指標で見た時と、別の指標で見た時には大きな違いがみられることもありますので、それぞれの指標を比べてみると多角的にジャーナルの評価をするのに役立つでしょう。
前回の記事で紹介した引用行動の悪い例を考えると、引用数を用いることに懐疑的になってしまいますが、とはいえ引用数が多いことに意味がないわけではありません。
多く引用される論文やジャーナルにはそれなりの理由があり、それらが業界内で批判的に吟味されている可能性も高まります。研究内容を理解して評価することが一番大事なのはもちろんですが、ある程度の質を担保するために数値を一助として活用するのは悪くないと思います。ただできれば上記に述べたような理由で複数の指標を並べてみるのが理想的ではないでしょうか。
また、AI技術の進化によって、引用の質を解析するツールがさらに発展すると予想されます。これらの新しい技術と従来の指標を組み合わせ、より多面的に評価できるようになってくると思われますが、それぞれの指標や引用行動を踏まえて自分がそのジャーナルや論文について何を評価しているのかを意識することが重要でしょう。ただ、一つの指標に基づいて出てくるようなオススメを鵜呑みにしていくのは望ましくないと言えます。
参考文献
- https://www.journalindicators.com/ ↩︎
- Ludo Waltman et al., “Some Modifications to the SNIP Journal Impact Indicator,” Journal of Informetrics 7, no. 2 (April 2013): 272–85, https://doi.org/10.1016/j.joi.2012.11.011. ↩︎
- https://www.youtube.com/watch?v=P8Kt6Abq_rM ↩︎
- https://clarivate.com/academia-government/scientific-and-academic-research/research-funding-analytics/journal-citation-reports/ ↩︎
- https://scholarlykitchen.sspnet.org/2008/07/23/eigenfactor/ ↩︎
- Jorge Mañana-Rodríguez, “A Critical Review of SCImago Journal & Country Rank,” Research Evaluation 24, no. 4 (October 2015): 343–54, https://doi.org/10.1093/reseval/rvu008. ↩︎
- J. E. Hirsch, “An Index to Quantify an Individual’s Scientific Research Output,” Proceedings of the National Academy of Sciences 102, no. 46 (November 15, 2005): 16569–72, https://doi.org/10.1073/pnas.0507655102. ↩︎











コメント